Kitabı oku: «William Oughtred», sayfa 2

ALLEGED TRAVEL ABROAD

According to certain sources of information, Oughtred traveled on the European Continent and was invited to change his abode to the Continent. We have seen no statement from Oughtred himself on this matter. He seldom referred to himself in his books and letters. The autobiography contained in his Apologeticall Epistle was written a quarter of a century before his death. Aubrey gives the following:

In the time of the civill warres the duke of Florence invited him over, and offered him 500 li. per annum; but he would not accept it, because of his religion.¹⁸

A portrait of Oughtred, painted in 1646 by Hollar and inserted in the English edition of the Clavis of 1647, contains underneath the following lines:

 
“Haec est Oughtredi senio labantis imago
Itala quam cupiit, Terra Britanna tulit.”
 

In the sketch of Oughtred by Owen Manning it is confessed that “it is not known to what this alludes; but possibly he might have been in Italy with his patron, the Earl of Arundel.”¹⁹ It would seem quite certain either that Oughtred traveled in Europe or that he received some sort of an offer to settle in Italy. In view of Aubrey’s explicit statement and of Oughtred’s well-known habit of confining himself to his duties and studies in his own parish, seldom going even as far as London, we strongly incline to the opinion that he did not travel on the Continent, but that he received an offer from some patron of the sciences – possibly some distinguished visitor – to settle in Italy.

HIS DEATH

He died at Albury, June 30, 1660, aged about eighty-six years. Of his last days and death, Aubrey speaks as follows:

Before he dyed he burned a world of papers, and sayd that the world was not worthy of them; he was so superb. He burned also severall printed bookes, and would not stirre, till they were consumed… I myselfe have his Pitiscus, imbelished with his excellent marginall notes, which I esteeme as a great rarity. I wish I could also have got his Bilingsley’s Euclid, which John Collins sayes was full of his annotations…

Ralph Greatrex, his great friend, the mathematicall instrument-maker, sayed he conceived he dyed with joy for the comeing-in of the king, which was the 29th of May before. “And are yee sure he is restored?” – “Then give me a glasse of sack to drinke his sacred majestie’s health.” His spirits were then quite upon the wing to fly away…²⁰

In this passage, as in others, due allowance must be made for Aubrey’s lack of discrimination. He was not in the habit of sifting facts from mere gossip. That Oughtred should have declared that the world was not worthy of his papers or manuscripts is not in consonance with the sweetness of disposition ordinarily attributed to him. More probable was the feeling that the papers he burned – possibly old sermons – were of no particular value to the world. That he did not destroy a large mass of mathematical manuscripts is evident from the fact that a considerable number of them came after his death into the hands of Sir Charles Scarborough, M.D., under whose supervision some of them were carefully revised and published at Oxford in 1677 under the title of Opuscula mathematica hactenus inedita.

Aubrey’s story of Oughtred’s mode of death has been as widely circulated in every modern biographical sketch as has his slander of Mrs. Oughtred by claiming that she was so penurious that she would deny him the use of candles to read by. Oughtred died on June 30; the Restoration occurred on May 29. No doubt Oughtred rejoiced over the Restoration, but the story of his drinking “a glass of sack” to his Majesty’s health, and then dying of joy is surely apocryphal. De Morgan humorously remarks, “It should be added, by way of excuse, that he was eighty-six years old.”²¹

CHAPTER II
PRINCIPAL WORKS

“CLAVIS MATHEMATICAE”

Passing to the consideration of Oughtred’s mathematical books, we begin with the observation that he showed a marked disinclination to give his writings to the press. His first paper on sun-dials was written at the age of twenty-three, but we are not aware that more than one brief mathematical manuscript was printed before his fifty-seventh year. In every instance, publication in printed form seems to have been due to pressure exerted by one or more of his patrons, pupils, or friends. Some of his manuscripts were lent out to his pupils, who prepared copies for their own use. In some instances they urged upon him the desirability of publication and assisted in preparing copy for the printer. The earliest and best-known book of Oughtred was his Clavis mathematicae, to which repeated allusion has already been made. As he himself informs us, he was employed by the Earl of Arundel about 1628 to instruct the Earl’s son, Lord William Howard (afterward Viscount Stafford) in the mathematics. For the use of this young man Oughtred composed a treatise on algebra which was published in Latin in the year 1631 at the urgent request of a kinsman of the young man, Charles Cavendish, a patron of learning.

The Clavis mathematicae,²² in its first edition of 1631, was a booklet of only 88 small pages. Yet it contained in very condensed form the essentials of arithmetic and algebra as known at that time.

Aside from the addition of four tracts, the 1631 edition underwent some changes in the editions of 1647 and 1648, which two are much alike. The twenty chapters of 1631 are reduced to nineteen in 1647 and in all the later editions. Numerous minute alterations from the 1631 edition occur in all parts of the books of 1647 and 1648. The material of the last three chapters of the 1631 edition is rearranged, with some slight additions here and there. The 1648 edition has no preface. In the print of 1652 there are only slight alterations from the 1648 edition; after that the book underwent hardly any changes, except for the number of tracts appended, and brief explanatory notes added at the close of the chapters in the English editions of 1694 and 1702. The 1652 and 1667 editions were seen through the press by John Wallis; the 1698 impression contains on the title-page the words: Ex Recognitione D. Johannis Wallis, S.T.D. Geometriae Professoris Saviliani.

The cost of publishing may be a matter of some interest. When arranging for the printing of the 1667 edition of the Clavis, Wallis wrote Collins: “I told you in my last what price she [Mrs. Lichfield] expects for it, as I have formerly understood from her, viz., £ 40 for the impression, which is about 9½d. a book.”²³

As compared with other contemporary works on algebra, Oughtred’s distinguishes itself for the amount of symbolism used, particularly in the treatment of geometric problems. Extraordinary emphasis was placed upon what he called in the Clavis the “analytical art.”²⁴ By that term he did not mean our modern analysis or analytical geometry, but the art “in which by taking the thing sought as knowne, we finde out that we seeke.”²⁵ He meant to express by it condensed processes of rigid, logical deduction expressed by appropriate symbols, as contrasted with mere description or elucidation by passages fraught with verbosity. In the preface to the first edition (1631) he says:

In this little book I make known.. the rules relating to fundamentals, collected together, just like a bundle, and adapted to the explanation of as many problems as possible.

As stated in this preface, one of his reasons for publishing the book, is

… that like Ariadne I might offer a thread to mathematical study by which the mysteries of this science might be revealed, and direction given to the best authors of antiquity, Euclid, Archimedes, the great geometrician Apollonius of Perga, and others, so as to be easily and thoroughly understood, their theorems being added, not only because to many they are the height and depth of mathematical science (I ignore the would-be mathematicians who occupy themselves only with the so-called practice, which is in reality mere juggler’s tricks with instruments, the surface so to speak, pursued with a disregard of the great art, a contemptible picture), but also to show with what keenness they have penetrated, with what mass of equations, comparisons, reductions, conversions and disquisitions these heroes have ornamented, increased and invented this most beautiful science.

The Clavis opens with an explanation of the Hindu-Arabic notation and of decimal fractions. Noteworthy is the absence of the words “million,” “billion,” etc. Though used on the Continent by certain mathematical writers long before this, these words did not become current in English mathematical books until the eighteenth century. The author was a great admirer of decimal fractions, but failed to introduce the notation which in later centuries came to be universally adopted. Oughtred wrote 0.56 in this manner 0|56; the point he used to designate ratio. Thus 3:4 was written by him 3·4. The decimal point (or comma) was first used by the inventor of logarithms, John Napier, as early as 1616 and 1617. Although Oughtred had mastered the theory of logarithms soon after their publication in 1614 and was a great admirer of Napier, he preferred to use the dot for the designation of ratio. This notation of ratio is used in all his mathematical books, except in two instances. The two dots (:) occur as symbols of ratio in some parts of Oughtred’s posthumous work, Opuscula mathematica hactenus inedita, Oxford, 1677, but may have been due to the editors and not to Oughtred himself. Then again the two dots (:) are used to designate ratio on the last two pages of the tables of the Latin edition of Oughtred’s Trigonometria of 1657. In all other parts of that book the dot (·) is used. Probably someone who supervised the printing of the tables introduced the (:) on the last two pages, following the logarithmic tables, where methods of interpolation are explained. The probability of this conjecture is the stronger, because in the English edition of the Trigonometrie, brought out the same year (1657) but after the Latin edition, the notation (:) at the end of the book is replaced by the usual (·), except that in some copies of the English edition the explanations at the end are omitted altogether.

Oughtred introduces an interesting, and at the same time new, feature of an abbreviated multiplication and an abbreviated division of decimal fractions. On this point he took a position far in advance of his time. The part on abbreviated multiplication was rewritten in slightly enlarged form and with some unimportant alterations in the later edition of the Clavis. We give it as it occurs in the revision. Four cases are given. In finding the product of 246|914 and 35|27, “if you would have the Product without any Parts” (without any decimal part), “set the place of Unity of the lesser under the place of Unity in the greater: as in the Example,” writing the figures of the lesser number in inverse order. From the example it will be seen that he begins by multiplying by 3, the right-hand digit of the multiplier. In the first edition of the Clavis he began with 7, the left digit. Observe also that he “carries” the nearest tens in the product of each lower digit and the upper digit one place to its right. For instance, he takes 7×4=28 and carries 3, then he finds 7×2+3=17 and writes down 17.

The second case supposes that “you would have the Product with some places of parts” (decimals), say 4: “Set the place of Unity of the lesser Number under the Fourth place of the Parts of the greater.” The multiplication of 246|914 by 35|27 is now performed thus:

In the third and fourth cases are considered factors which appear as integers, but are in reality decimals; for instance, the sine of 54° is given in the tables as 80902 when in reality it is .80902.

Of interest as regards the use of the word “parabola” is the following: “The Number found by Division is called the Quotient, or also Parabola, because it arises out of the Application of a plain Number to a given Longitude, that a congruous Latitude may be found.”²⁶ This is in harmony with etymological dictionaries which speak of a parabola as the application of a given area to a given straight line. The dividend or product is the area; the divisor or factor is the line.

Oughtred gives two processes of long division. The first is identical with the modern process, except that the divisor is written below every remainder, each digit of the divisor being crossed out as soon as it has been used in the partial multiplication. The second method of long division is one of the several types of the old “scratch method.” This antiquated process held its place by the side of the modern method in all editions of the Clavis. The author divides 467023 by 357|0926425, giving the following instructions: “Take as many of the first Figures of the Divisor as are necessary, for the first Divisor, and then in every following particular Division drop one of the Figures of the Divisor towards the Left Hand, till you have got a competent Quotient.” He does not explain abbreviated division as thoroughly as abbreviated multiplication.

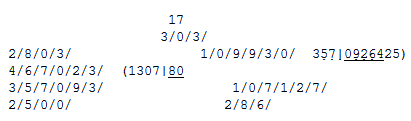
Oughtred does not examine the degree of reliability or accuracy of his processes of abbreviated multiplication and division. Here as in other places he gives in condensed statement the mode of procedure, without further discussion.

He does not attempt to establish the rules for the addition, subtraction, multiplication, and division of positive and negative numbers. “If the Signs are both alike, the Product will be affirmative, if unlike, negative”; then he proceeds to applications. This attitude is superior to that of many writers of the eighteenth and nineteenth centuries, on pedagogical as well as logical grounds: pedagogically, because the beginner in the study of algebra is not in a position to appreciate an abstract train of thought, as every teacher well knows, and derives better intellectual exercise from the applications of the rules to problems; logically, because the rule of signs in multiplication does not admit of rigorous proof, unless some other assumption is first made which is no less arbitrary than the rule itself. It is well known that the proofs of the rule of signs given by eighteenth-century writers are invalid. Somewhere they involve some surreptitious assumption. This criticism applies even to the proof given by Laplace, which tacitly assumes the distributive law in multiplication.

A word should be said on Oughtred’s definition of + and – . He recognizes their double function in algebra by saying (Clavis, 1631, p. 2): “Signum additionis, sive affirmationis, est + plus” and “Signum subductionis, sive negationis est – minus.” They are symbols which indicate the quality of numbers in some instances and operations of addition or subtraction in other instances. In the 1694 edition of the Clavis, thirty-four years after the death of Oughtred, these symbols are defined as signifying operations only, but are actually used to signify the quality of numbers as well. In this respect the 1694 edition marks a recrudescence.

The characteristic in the Clavis that is most striking to a modern reader is the total absence of indexes or exponents. There is much discussion in the leading treatises of the latter part of the sixteenth and the early part of the seventeenth century on the theory of indexes, but the modern exponential notation, aⁿ, is of later date. The modern notation, for positive integral exponents, first appears in Descartes’ Géométrie, 1637; fractional and negative exponents were first used in the modern form by Sir Isaac Newton, in his announcement of the binomial formula, in a letter written in 1676. This total absence of our modern exponential notation in Oughtred’s Clavis gives it a strange aspect. Like Vieta, Oughtred uses ordinarily the capital letters, A, B, C… to designate given numbers; A² is written Aq, A³ is written Ac; for A⁴, A⁵, A⁶ he has, respectively, Aqq, Aqc, Acc. Only on rare occasions, usually when some parallelism in notation is aimed at, does he use small letters²⁷ to represent numbers or magnitudes. Powers of binomials or polynomials are marked by prefixing the capital letters Q (for square), C (for cube), QQ (for the fourth power), QC (for the fifth power), etc.

Oughtred does not express aggregation by (). Parentheses had been used by Girard, and by Clavius as early as 1609,²⁸ but did not come into general use in mathematical language until the time of Leibniz and the Bernoullis. Oughtred indicates aggregation by writing a colon (:) at both ends. Thus, Q:A-E: means with him (A-E)². Similarly, √q:A+E: means √(A+E). The two dots at the end are frequently omitted when the part affected includes all the terms of the polynomial to the end. Thus, C:A+B-E=.. means (A+B-E)³=.. There are still further departures from this notation, but they occur so seldom that we incline to the interpretation that they are simply printer’s errors. For proportion Oughtred uses the symbol (::). The proportion a:b=c:d appears in his notation a·b::c·d. Apparently, a proportion was not fully recognized in this day as being the expression of an equality of ratios. That probably explains why he did not use = here as in the notation of ordinary equations. Yet Oughtred must have been very close to the interpretation of a proportion as an equality; for he says in his Elementi decimi Euclidis declaratio, “proportio, sive ratio aequalis ::” That he introduced this extra symbol when the one for equality was sufficient is a misfortune. Simplicity demands that no unnecessary symbols be introduced. However, Oughtred’s symbolism is certainly superior to those which preceded. Consider the notation of Clavius.²⁹ He wrote 20:60=4:x, x=12, thus: “20·60·4? fiunt 12.” The insufficiency of such a notation in the more involved expressions frequently arising in algebra is readily seen. Hence Oughtred’s notation (::) was early adopted by English mathematicians. It was used by John Wallis at Oxford, by Samuel Foster at Gresham College, by James Gregory of Edinburgh, by the translators into English of Rahn’s algebra, and by many other early writers. Oughtred has been credited generally with the introduction of St. Andrew’s cross × as the symbol for multiplication in the Clavis of 1631. We have discovered that this symbol, or rather the letter x which closely resembles it, occurs as the sign of multiplication thirteen years earlier in an anonymous “Appendix to the Logarithmes, shewing the practise of the Calculation of Triangles etc.” to Edward Wright’s translation of John Napier’s Descriptio, published in 1618.³⁰ Later we shall give our reasons for believing that Oughtred is the author of that “Appendix.” The × has survived as a symbol of multiplication.

Another symbol introduced by Oughtred and found in modern books is ~, expressing difference; thus C~D signifies the difference between C and D, even when D is the larger number.³¹ This symbol was used by John Wallis in 1657.³²

Oughtred represented in symbols also certain composite expressions, as for instance A+E=Z, A-E=X, where A is greater than E. He represented by a symbol also each of the following: A²+E², A³+E³, A²-E², A³-E³.

Oughtred practically translated the tenth book of Euclid from its ponderous rhetorical form into that of brief symbolism. An appeal to the eye was a passion with Oughtred. The present writer has collected the different mathematical symbols used by Oughtred and has found more than one hundred and fifty of them.

The differences between the seven different editions of the Clavis lie mainly in the special parts appended to some editions and dropped in the latest editions. The part which originally constituted the Clavis was not materially altered, except in two or three of the original twenty chapters. These changes were made in the editions of 1647 and 1648. After the first edition, great stress was laid upon the theory of indices upon the very first page, as also in passages farther on. Of course, Oughtred did not have our modern notation of indices or exponents, but their theory had been a part of algebra and arithmetic for some time. Oughtred incorporated this theory in his brief exposition of the Hindu-Arabic notation and in his explanation of logarithms. As previously pointed out, the last three chapters of the 1631 edition were considerably rearranged in the later editions and combined into two chapters, so that the Clavis proper had nineteen chapters instead of twenty in the additions after the first. These chapters consisted of applications of algebra to geometry and were so framed as to constitute a severe test of the student’s grip of the subject. The very last problem deals with the division of angles into equal parts. He derives the cubic equation upon which the trisection depends algebraically, also the equations of the fifth degree and seventh degree upon which the divisions of the angle into 5 and 7 equal parts depend, respectively. The exposition was severely brief, yet accurate. He did not believe in conducting the reader along level paths or along slight inclines. He was a guide for mountain-climbers, and woe unto him who lacked nerve.

Oughtred lays great stress upon expansions of powers of a binomial. He makes use of these expansions in the solution of numerical equations. To one who does not specialize in the history of mathematics such expansions may create surprise, for did not Newton invent the binomial theorem after the death of Oughtred? As a matter of fact, the expansions of positive integral powers of a binomial were known long before Newton, not only to seventeenth-century but even to eleventh-century mathematicians. Oughtred’s Clavis of 1631 gave the binomial coefficients for all powers up to and including the tenth. What Newton really accomplished was the generalization of the binomial expansion which makes it applicable to negative and fractional exponents and converts it into an infinite series.

As a specimen of Oughtred’s style of writing we quote his solution of quadratic equations, accompanied by a translation into English and into modern mathematical symbols.

As a preliminary step³³ he lets

Z=A+E and A>E;

he lets also X=A-E. From these relations he obtains identities which, in modern notation, are ¼Z²-AE=(½Z-E)²=¼X². Now, if we know Z and AE, we can find ½X. Then ½(Z+X)=A, and ½(Z-X)=E, and

A=½Z+√¼Z²-AE.

Having established these preliminaries, he proceeds thus:

Datis igitur linea inaequaliter secta Z (10), & rectangulo sub segmentis AE (21) qui gnomon est: datur semidifferentia segmentorum ½X: & per consequens ipsa segmenta. Nam ponatur alterutrum segmentum A: alterum erit Z-A: Rectangulum auctem est ZA-Aq=AE. Et quia dantur Z & AE: estque ¼Zq-AE=¼Xq: & per 5c. 18, ½Z+½X=A: & ½Z-½X=E: Aequatio sic resoluetur: ½Z±√q:¼Zq-AE:=A

Itaque proposita equatione, in qua sunt tres species aequaliter in ordine tabellae adscendentes, altissima autem species ponitur negata: Magnitudo data coefficiens mediam speciem est linea bisecanda: & magnitudo absoluta data, ad quam sit aequatio, est rectangulum sub segmentis inaequalibus, sine gnomon: vt ZA-Aq=AE: in numeris autem 10l-lq=21: Estque A, vel 1l, alterutrum segmentum inaequale. Inuenitur autem sic:

Dimidiata coefficiens median speciem est

(5); cuius quadratum est

(25): ex hoc tolle AE (21) absolutum: eritque

(4) quadratum semidifferentiae segmentorum: latus huius quadratum (2) est semidifferentia: quam si addas ad

(5) semissem coefficientis, sive lineae bisecandae, erit maius segment.; sin detrahas, erit minus segment: Dico

We translate the Latin passage, using the modern exponential notation and parentheses, as follows:

Given therefore an unequally divided line Z (10), and a rectangle beneath the segments AE (21) which is a gnomon. Half the difference of the segments ½X is given, and consequently the segment itself. For, if one of the two segments is placed equal to A, the other will be Z-A. Moreover, the rectangle is ZA-A²=AE. And because Z and AE are given, and there is ¼Z²-AE=¼X², and by 5c.18, ½Z+½X=A, and ½Z-½X=E, the equation will be solved thus: ½Z±√(¼Z²-AE)=A

And so an equation having been proposed in which three species (terms) are in equally ascending powers, the highest species, moreover, being negative, the given magnitude which constitutes the middle species is the line to be bisected. And the given absolute magnitude to which it is equal is the rectangle beneath the unequal segments, without gnomon. As ZA-A²=AE, or in numbers, 10x-x²=21. And A or x is one of the two unequal segments. It may be found thus:

The half of the middle species is

(5), its square is

(25). From it subtract the absolute term AE (21), and

(4) will be the square of half the difference of the segments. The square root of this,

(2), is half the difference. If you add it to half the coefficient

(5), or half the line to be bisected, the longer segment is obtained; if you subtract it, the smaller segment is obtained. I say:

The quadratic equation Aq+ZA=AE receives similar treatment. This and the preceding equation, ZA-Aq=AE, constitute together a solution of the general quadratic equation, x²+ax=b, provided that E or Z are not restricted to positive values, but admit of being either positive or negative, a case not adequately treated by Oughtred. Imaginary numbers and imaginary roots receive no consideration whatever.

A notation suggested by Vieta and favored by Girard made vowels stand for unknowns and consonants for knowns. This conventionality was adopted by Oughtred in parts of his algebra, but not throughout. Near the beginning he used Q to designate the unknown, though usually this letter stood with him for the “square” of the expression after it.³⁴

It is of some interest that Oughtred used

to signify the ratio of the circumference to the diameter of a circle. Very probably this notation is the forerunner of the π=3.14159.. used in 1706 by William Jones. Oughtred first used

in the 1647 edition of the Clavis mathematicae. In the 1652 edition he says, “Si in circulo sit 7.22::δ·π::113.355: erit δ·π::2 R.P: periph.” This notation was adopted by Isaac Barrow, who used it extensively. David Gregory³⁵ used

in 1697, and De Moivre³⁶ used

about 1697, to designate the ratio of the circumference to the radius.

We quote the description of the Clavis that was given by Oughtred’s greatest pupil, John Wallis. It contains additional information of interest to us. Wallis devotes chap. xv of his Treatise of Algebra, London, 1685, pp. 67-69, to Mr. Oughtred and his Clavis, saying:

Mr. William Oughtred (our Country-man) in his Clavis Mathematicae, (or Key of Mathematicks,) first published in the Year 1631, follows Vieta (as he did Diophantus) in the use of the Cossick Denominations; omitting (as he had done) the names of Sursolids, and contenting himself with those of Square and Cube, and the Compounds of these.

But he doth abridge Vieta’s Characters or Species, using only the letters q, c, &c. which in Vieta are expressed (at length) by Quadrate, Cube, &c. For though when Vieta first introduced this way of Specious Arithmetick, it was more necessary (the thing being new,) to express it in words at length: Yet when the thing was once received in practise, Mr. Oughtred (who affected brevity, and to deliver what he taught as briefly as might be, and reduce all to a short view,) contented himself with single Letters instead of those words.

Thus what Vieta would have written

would with him be thus expressed

And the better to distinguish upon the first view, what quantities were Known, and what Unknown, he doth (usually) denote the Known to Consonants, and the Unknown by Vowels; as Vieta (for the same reason) had done before him.

He doth also (to very great advantage) make use of several Ligatures, or Compendious Notes, to signify Summs, Differences, and Rectangles of several Quantities. As for instance, Of two Quantities A (the Greater), and E (the Lesser), the Sum he calls Z, the Difference X, the Rectangle AE…

Which being of (almost) a constant signification with him throughout, do save a great circumlocution of words, (each Letter serving instead of a Definition;) and are also made use of (with very great advantage) to discover the true nature of divers intricate Operations, arising from the various compositions of such Parts, Sums, Differences, and Rectangles; (of which there is great plenty in his Clavis, Cap. 11, 16, 18, 19. and elsewhere,) which without such Ligatures, or Compendious Notes, would not be easily discovered or apprehended…

I know there are who find fault with his Clavis, as too obscure, because so short, but without cause; for his words be always full, but not Redundant, and need only a little attention in the Reader to weigh the force of every word, and the Syntax of it;.. And this, when once apprehended, is much more easily retained, than if it were expressed with the prolixity of some other Writers; where a Reader must first be at the pains to weed out a great deal of superfluous Language, that he may have a short prospect of what is material; which is here contracted for him in a short Synopsis…

Mr. Oughtred in his Clavis, contents himself (for the most part) with the solution of Quadratick Equations, without proceeding (or very sparingly) to Cubick Equations, and those of Higher Powers; having designed that Work for an Introduction into Algebra so far, leaving the Discussion of Superior Equations for another work… He contents himself likewise in Resolving Equations, to take notice of the Affirmative or Positive Roots; omitting the Negative or Ablative Roots, and such as are called Imaginary or Impossible Roots. And of those which, he calls Ambiguous Equations, (as having more Affirmative Roots than one,) he doth not (that I remember) any where take notice of more than Two Affirmative Roots: (Because in Quadratick Equations, which are those he handleth, there are indeed no more.) Whereas yet in Cubick Equations, there may be Three, and in those of Higher Powers, yet more. Which Vieta was well aware of, and mentioneth in some of his Writings; and of which Mr. Oughtred could not be ignorant.