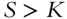Kitabı oku: «The Unlucky Investor's Guide to Options Trading», sayfa 2

Chapter 1
Math and Finance Preliminaries

The purpose of this book is to provide a qualitative framework for options investing based on a quantitative analysis of financial data and theory. Mathematics plays a crucial role when developing this framework, but it is predominantly a means to an end. This chapter therefore includes a brief overview of the prerequisite math and financial concepts required to understand this book. Because this isn't in‐depth coverage of the following topics, we encourage you to explore the supplemental texts listed in the references section for those mathematically inclined. Formulae and their descriptions are included in several sections for reference, but they are not necessary to follow the remainder of the book.

Stocks, Exchange‐Traded Funds, and Options

From swaptions to non‐fungible tokens (NFTs), new instruments and opportunities frequently emerge as markets evolve. By the time this book reaches the shelf, the financial landscape and the instruments occupying it may be very different from when it was written. Rather than focus on a wide range of instruments, this book discusses fundamental trading concepts using a small selection of asset classes (stocks, exchange‐traded funds, and options) to formulate examples.

A share of stock is a security that represents a fraction of ownership of a corporation. Stock shares are normally issued by the corporation as a source of funding, and these instruments are usually publicly traded on stock exchanges, such as the New York Stock Exchange (NYSE) and the Nasdaq. Shareholders are entitled to a fraction of the company's assets and profits based on the proportion of shares they own relative to the number of outstanding shares.

An exchange‐traded fund (ETF) is a basket of securities, such as stocks, bonds, or commodities. Like stocks, shares of ETFs are traded publicly on stock exchanges. Similar to mutual funds, these instruments represent a fraction of ownership of a diversified portfolio that is usually managed professionally. These assets track aspects of the market such as an index, sector, industry, or commodity. For example, SPDR S&P 500 (SPY) is a market index ETF tracking the S&P 500, Energy Select Sector SPDR Fund (XLE) is a sector ETF tracking the energy sector, and SPDR Gold Trust (GLD) is a commodity ETF tracking gold. ETFs are typically much cheaper to trade than the individual assets in an ETF portfolio and are inherently diversified. For instance, a share of stock for an energy company is subject to company‐specific risk factors, while a share of an energy ETF is diversified over several energy companies.

When assessing the price dynamics of a stock or ETF and comparing the dynamics of different assets, it is common to convert price information into returns. The return of a stock is the amount the stock price increased or decreased as a proportion of its value rather than a dollar amount. Returns can be scaled over any time frame (daily, monthly, annual), with calculations typically calling for daily returns. The two most common types of returns are simple returns, represented as a percentage and calculated using Equation (1.1), and log returns, calculated using Equation (1.2). The logarithm's mathematical definition and properties are covered in the appendix for those interested, but that information is not necessary to know to follow the remainder of the book.

(1.1)

(1.2)

where is the price of the asset on day t and is the price of the asset the prior day. For example, an asset priced at $100 on day 1 and $101 on day 2 has a simple daily return of 0.01 (1%) and a log return of 0.00995. Simple and log returns have different mathematical characteristics (e.g., log returns are time‐additive), which impact more advanced quantitative analysis. However, these factors are not relevant for the purposes of this book because the difference between log returns and simple returns is fairly negligible when working on daily timescales. Simple daily returns are used for all returns calculations shown.

An option is a type of financial derivative, meaning its price is based on the value of an underlying asset. Options contracts are either traded on public exchanges (exchange‐traded options) or traded privately with little regulatory oversight (over‐the‐counter [OTC] options). As OTC options are nonstandardized and usually inaccessible for retail investors, only exchange‐traded options will be discussed in this book.

An option gives the holder the right (but not the obligation) to buy or sell some amount of an underlying asset, such as a stock or ETF, at a predetermined price on or before a future date. The two most common styles of options are American and European options. American options can be exercised at any point prior to expiration, and European options can only be exercised on the expiration date.¹ Because American options are generally more popular than European options and offer more flexibility, this book focuses on American options.

The most basic types of options are calls and puts. American calls give the holder the right to buy the underlying asset at a certain price within a given time frame, and American puts give the holder the right to sell the underlying asset. The contract parameters must be specified prior to opening the trade and are listed below:

● The underlying asset trading at the spot price, or the current per share price .

● The number of underlying shares. One option usually covers 100 shares of the underlying, known as a one lot.

● The price at which the underlying shares can be bought or sold prior to expiration. This price is called the strike price .

● The expiration date, after which the contract is worthless. The time between the present day and the expiration date is the contract's duration or days to expiration (DTE).

Note that the price of the option is commonly denoted as C for calls, P for puts, and V if the type of contract is not specified. Options traders may buy or sell these contracts, and the conditions for profitability differ depending on the choice of position. The purchaser of the contract pays the option premium (current market price of the option) to adopt the long side of the position. This is also known as a long premium trade. The seller of the contract receives the option premium to adopt the short side of the position, thus placing a short premium trade. The choice of strategy corresponds to the directional assumption of the trader. For calls and puts, the directional assumption is either bullish, assuming the underlying price will increase, or bearish, assuming the underlying price will decrease. The directional assumptions and scenarios for profitability for these contracts are summarized in the following table.

Table 1.1 The definitions, conditions for profitability, and directional assumptions for long/short calls/puts.

The relationship between the strike price and the current price of the underlying determines the moneyness of the position. This is equivalently the intrinsic value of a position, or the value of the contract if it were exercised immediately. Contracts can be described as one of the following, noting that options cannot have negative intrinsic value:

● In‐the‐money (ITM): The contract would be profitable if it was exercised immediately and thus has intrinsic value.

● Out‐of‐the‐money (OTM): The contract would result in a loss if it was exercised immediately and thus has no intrinsic value.

● At‐the‐money (ATM): The contract has a strike price equal to the price of the underlying and thus has no intrinsic value.

The intrinsic value of a position is based entirely on the type of position and the choice of strike price relative to the price of the underlying:

● Call options

● Intrinsic Value = Either (stock price – strike price) or 0

● ITM:

● OTM:

● ATM:

● Put options

● Intrinsic Value = Either or 0

● ITM:

● OTM:

● ATM:

For example, consider a 45 DTE put contract with a strike price of $100:

● Scenario 1 (ITM): The underlying price is $95. In this case, the intrinsic value of the put contract is $5 per share.

● Scenario 2 (OTM): The underlying price is $105. In this case, the put contract has no intrinsic value.

● Scenario 3 (ATM): The underlying price is $100. In this case, the put is also considered to have no intrinsic value.

The value of an option also depends on speculative factors, driven by supply and demand. The extrinsic value of the option is the difference between the current market price for the option and the intrinsic value of the option. Again, consider a 45 DTE put contract with a strike price of $100 on an underlying with a current price per share of $105. Suppose that, due to a period of recent market turbulence, investors are fearful the underlying price will crash within the next 45 days and create a demand for these OTM put contracts. The surge in demand inflates the price of the put contract to $10 per share. Therefore, because the put contract has no intrinsic value but has a market price of $10, the extrinsic value of the contract is $10 per share. If, instead, the price of the underlying is $95 and the price of the ITM put is still $10 per share, then the contract will have $5 in intrinsic value and $5 in extrinsic value.

The profitability of an option ultimately depends on both intrinsic and extrinsic factors, and it is calculated as the difference between the intrinsic value of an option and the cost of the contract. Mathematically, profit and loss (P/L) approximations for long calls and puts at exercise are given by the following equations:²

(1.3)

(1.4)

where the max function simply outputs the larger of the two values. For instance, equals 1 while equals 0. The P/Ls for the corresponding short sides are merely Equations (1.3) and (1.4) multiplied by –1. Following is a sample trade that applies the long call profit formula.

Example trade: A call with 45 DTE duration is traded on an underlying that is currently priced at $100 . The strike price is $105 and the long call is currently valued at $100 per one lot ($1 per share).

● Scenario 1: The underlying increases to $105 by the expiration date.

● Long call P/L:

● Short call P/L: +$100.

● Scenario 2: The underlying increases to $110 by the expiration date.

● Long call P/L:

● Short call P/L: –$400.

● Scenario 3: The underlying decreases to $95 by the expiration date.

● Long call P/L:

● Short call P/L: +$100.

The trader adopting the long position pays the seller the option premium upfront and profits when the intrinsic value exceeds the price of the contract. The short trader profits when the intrinsic value remains below the price of the contract, especially when the position expires worthless (no intrinsic value). The extrinsic value of an option generally decreases over the duration of the contract, as uncertainty around the underlying price and uncertainty around the profit potential of the option decrease. As a position nears expiration, the price of an option converges toward its intrinsic value.

Options pricing clearly plays a large role in options trading. To develop an intuitive understanding around how options are priced, understanding the mathematical assumptions around market efficiency and price dynamics is critical.

The Efficient Market Hypothesis

Traders must make a number of assumptions prior to placing a trade. Options traders must make directional assumptions about the price of the underlying over a given time frame: bearish (expecting price to decrease), bullish (expecting price to increase), or neutral (expecting price to remain relatively unchanged). Options traders also must make assumptions about the current value of an option. If options contracts are perceived as overvalued, long positions are less likely to profit. If options contracts are perceived as undervalued, short positions are less likely to profit. These assumptions about underlying and option price dynamics are a personal choice, but traders can formulate consistent assumptions by referring to the efficient market hypothesis (EMH). The EMH states that instruments are traded at a fair price, and the current price of an asset reflects some amount of available information. The hypothesis comes in three forms:

1. Weak EMH: Current prices reflect all past price information.

2. Semi‐strong EMH: Current prices reflect all publicly available information.

3. Strong EMH: Current prices reflect all possible information.

No variant of the EMH is universally accepted or rejected. The form that a trader assumes is subjective, and methods of market analysis available are limited depending on that choice. Proponents of the strong EMH posit that investors benefit from investing in low‐cost passive index funds because the market is unbeatable. Opponents believe the market is beatable by exploiting inefficiencies in the market. Traders who accept the weak EMH believe technical analysis (using past price trends to predict future price trends) is invalidated, but fundamental analysis (using related economic data to predict future price trends) is still viable. Traders who accept the semi‐strong EMH assume fundamental analysis would not yield systematic success but trading according to private information would. Traders who accept the strong EMH maintain that even insider trading will not result in consistent success and no exploitable market inefficiencies are available to anyone.

This book focuses on highly liquid markets, and inefficiencies are assumed to be minimal. More specifically, this book assumes a semi‐strong form of the EMH. Rather than constructing portfolios according to forecasts of future price trends, the purpose of this text is to demonstrate how trading options according to current market conditions and directional volatility assumptions (rather than price assumptions) has allowed options sellers to consistently outperform the market.

This “edge” is not the result of some inherent market inefficiency but rather a trade‐off of risk. Recall the example long call trade from the previous section. Notice that there are more scenarios in which the short trader profits compared to the long trader. Generally, short premium positions are more likely to yield a profit compared to long premium positions. This is because options are assumed to be priced efficiently and scaled according to the perceived risk in the market, meaning that long positions only profit when the underlying has large directional moves outside of expectations. As these types of events are uncommon, options contracts go unused the majority of the time and short premium positions profit more often than long positions. However, when those large, unexpected moves do occur, the short premium positions are subject to potentially massive losses. The risk profiles for options are complex, but they can be intuitively represented with probability distributions.

Probability Distributions

To better understand the risk profiles of short options, this book utilizes basic concepts from probability theory, specifically random variables and probability distributions. Random variables are formal stand‐ins for uncertain quantities. The probability distribution of a random variable describes possible values of that quantity and the likelihood of each value occurring. Generally, probability distributions are represented by the symbol P , which can be read as “the probability that.” For example, . Random variables and probability distributions are tools for working with probabilistic systems (i.e., systems with many unpredictable outcomes), such as stock prices. Although future outcomes cannot be precisely predicted, understanding the distribution of a probabilistic system makes it possible to form expectations about the future, including the uncertainty associated with those expectations.

Let's begin with an example of a simple probabilistic system: rolling a pair of fair, six‐sided dice. In this case, if D represents the sum of the dice, then D is a random variable with 11 possible values ranging from 2 to 12. Some of these outcomes are more likely than others. Since, for instance, there are more ways to roll a sum of 7 ([1,6], [2,5], [3,4], [4,3], [5,2], [6,1]) than a sum of 10 ([4,6], [5,5], [6,4]), there is a higher probability of rolling a 7 than a 10. Observing that there are 36 possible rolls ([1,1], [1,2], [2,1], etc.) and that each is equally likely, one can use symbols to be more precise about this:

The distribution of D can be represented elegantly using a histogram. These types of graphs display the frequency of different outcomes, grouped according to defined ranges. When working with measured data, histograms are used to estimate the true underlying probability distribution of a probabilistic system. For this fair dice example, there will be 11 bins, corresponding to the 11 possible outcomes. This histogram is shown below in Figure 1.1, populated with data from 100,000 simulated dice rolls.

Figure 1.1 A histogram for 100,000 simulated rolls for a pair of fair dice. This diagram shows the likelihood of each outcome occurring according to this simulation (e.g., the height of the bin ranging from 6.5 to 7.5 is near 17%, indicating that 7 occurred nearly 17% of the time in the 100,000 trials).

Distributions like the ones shown here can be summarized using quantitative measures called moments.³ The first two moments are mean and variance.

Mean (first moment): Also known as the average and represented by the Greek letter μ (mu), this value describes the central tendency of a distribution. This is calculated by summing all the observed outcomes together and dividing by the number of observations :

(1.5)

For distributions based on statistical observations with a sufficiently large number of occurrences, the mean corresponds to the expected value of that distribution. The expected value of a random variable is the weighted average of outcomes and the anticipated average outcome over future trials. The expected value of a random variable X , denoted , can be estimated using statistical data and Equation (1.5), or if the unique outcomes () and their respective probabilities are known, then the expected value can also be calculated using the following formula:

(1.6)

In the dice sum example, represented with random variable D , the possible outcomes (2, 3, 4, …, 12) and the probability of each occurring (2.78%, 5.56%, 8.33%, …, 2.78%) are known, so the expected value can be determined as follows:

The theoretical long‐term average sum is seven. Therefore, if this experiment is repeated many times, the mean of the observations calculated using Equation (1.5) should yield an output close to seven.

Variance (second moment): This is the measure of the spread, or variation, of the data points from the mean of the distribution. Standard deviation, represented with by the Greek letter σ (sigma), is the square root of variance and is commonly used as a measure of uncertainty (equivalently, risk or volatility). Distributions with more variance are wider and have more uncertainty around future outcomes. Variance is calculated according to the following:⁴

(1.7)

When a large portion of data points are dispersed far from the mean, the variance of the entire set is large, and uncertainty on measurements from that system is significant. The variance of a random variable X, denoted (X), can also be calculated in terms of the expected value, E [X]:

(1.8)

For the dice sum random variable, D, the possible outcomes (2, 3, 4, …, 12) and the probability of each occurring (2.78%, 5.56%, 8.33%, …, 2.78%) are known, so the variance of this experiment is as follows:

This equation indicates that the spread of the distribution for this random variable is around 5.84 and the uncertainty (standard deviation) is approximately 2.4 (shown in Figure 1.2).

One can compare these theoretical estimates for the mean and standard deviation of the dice sum experiment to the values measured from statistical data. The calculated first and second moments from the simulated dice roll experiment are plotted in Figure 1.2 for comparison.

Obtaining a distribution average near 7.0 makes intuitive sense because 7 is the most likely sum to roll out of the possible outcomes. The standard deviation indicates that the uncertainty associated with that expected value is near 2.4. Inferring from the shape of the distribution, which has most of the probability mass concentrated near the center, one can conclude that on any given roll the outcome will most likely fall between five and nine.

The distribution just shown is symmetric about the mean, but probability distributions are often asymmetric. To quantify the degree of asymmetry for a distribution, the third moment is used.

Skew (third moment): This is a measure of the asymmetry of a distribution. A distribution's skew can be positive, negative, or zero and depends on whether the tail to the right of the mean is larger (positive skew), to the left is larger (negative skew), or equal on both sides (zero skew). Unlike mean and standard deviation, which have units defined by the random variable, skew is a pure number that quantifies the degree of asymmetry according to the following formula:

(1.9)

Figure 1.2 A histogram for 100,000 simulated dice rolls with fair dice. Included is the mean of the distribution (solid line) and the standard deviation of the distribution on either side of the mean (dotted line), both calculated using the observations from the simulated experiment. The average of this distribution was 7.0 and the standard deviation was 2.4, consistent with the theoretical estimates.

The concept of skew and its applications can be best understood with a modification to the dice rolling example. Suppose that the dice are biased rather than fair. Let's consider two scenarios: a pair of unfair dice with a small number bias (two and three more likely) and a pair of unfair dice with a large number bias (four and five more likely). The probabilities of each number appearing on each die for the different cases are shown in Table 1.2.

Table 1.2 The probability of each number appearing on each die in the three different scenarios, one fair and two unfair.

When rolling the fair pair and plotting the histogram of the possible sums, the distribution is symmetric about the mean and has a skew of zero. However, the distributions when rolling the unfair dice are skewed, as shown in Figures 1.3(a) and (b).

The skew of a distribution is classified according to where the majority of the distribution mass is concentrated. Remember that the positive side is to the right of the mean and the negative side is to the left. The histogram in Figure 1.3(a) has a longer tail on the positive side and has the most mass concentrated on the negative side of the mean: This is an example of positive skew (skew = 0.45). The histogram in Figure 1.3(b) has a longer tail on the negative side and has the majority of the mass concentrated on the positive side of the mean: This is an example of negative skew (skew = –0.45).

When a distribution has skew, the interpretation of standard deviation changes. In the example with fair dice, the expected value of the experiment is 2.4, suggesting that any given trial will most likely have an outcome between five and nine. This is a valid interpretation because the distribution is symmetric about the mean and most of the distribution mass is concentrated around it. However, consider the distribution in the unfair example with the large number bias. This distribution has a mean of 7.8 and a standard deviation of 2.0, naively suggesting that the outcome will most likely be between six and nine with the outcomes on either side being equally probable. However, because the majority of the occurrences are concentrated on the positive side of the mean (roughly 60% of occurrences), the uncertainty is not symmetric. This concept will be discussed in more detail in a later chapter, as distributions of financial instruments are commonly skewed, and there is ambiguity in defining risk under those circumstances.

Figure 1.3 (a) A histogram for 100,000 simulated dice rolls with unfair dice, biased such that smaller numbers (2 and 3) are more likely to appear on each die. (b) A histogram for 100,000 simulated dice rolls with unfair dice, biased such that larger numbers (4 and 5) are more likely to appear on each die.

Mathematicians and scientists have encountered some probability distributions repeatedly in theory and applications. These distributions have, in turn, received a great deal of study. Assuming the underlying distribution of an experiment resembles a well known form can often greatly simplify statistical analysis. The normal distribution (also known as the Gaussian distribution or the bell curve) is arguably one of the most well‐known probability distributions and foundational in quantitative finance. It describes countless different real‐world systems because of a result known as the central limit theorem. This theorem says, roughly, that if a random variable is made by adding together many independently random pieces, then, regardless of what those pieces are, the result will be normally distributed. For example, the distribution in the two‐dice example is fairly non‐normal, being relatively triangular and lacking tails. If one considered the sum of more and more dice, each of which is an independent random variable, the distribution would gradually take on a bell shape. This is shown in Figure 1.4.

The normal distribution is a symmetric, bell‐shaped distribution, meaning that equidistant events on either side of the center are equally likely and the skew is zero. The distribution is centered around the mean, and outcomes further away from the mean are less likely. The normal distribution has the intriguing property that 68% of occurrences fall within of the mean, 95% of occurrences are within of the mean, and 99.7% of occurrences are within of the mean. Figure 1.5 plots a normal distribution.

These probabilities can be used to roughly contextualize distributions with similar geometry. For example, in the fair dice pair model, the expected value of the fair dice experiment was 7.0, and the standard deviation was 2.4. With the assumption of normality, one would infer there is roughly a 68% chance that future outcomes will fall between five and nine. The true probability is 66.67% for this random variable, indicating that the normality assumption is not exactly correct but can be used for the purposes of approximation. As more dice are added to the example, this approximation becomes increasingly accurate.

Figure 1.4 A histogram for 100,000 simulated rolls with a group of fair, six‐sided dice numbering (a) 2, (b) 4, or (c) 6.

Understanding distribution statistics and the properties of the normal distribution is incredibly useful in quantitative finance. The expected return of a stock is usually estimated by the mean return, and the historic risk is estimated with the standard deviation of returns (historical volatility). Stock log returns are also widely assumed to be normally distributed. Although, this is only approximately true because the overwhelming majority of stocks and ETFs have skewed returns distributions.⁵ Regardless, this normality estimation provides a quantitative framework for expectations around future price moments. This approximation also simplifies mathematical models of price dynamics and options pricing, the most notable of which is the Black‐Scholes model.

Figure 1.5 A detailed plot of the normal distribution and the corresponding probabilities at each standard deviation mark.