Kitabı oku: «The Unlucky Investor's Guide to Options Trading», sayfa 3

The Black‐Scholes Model

The Black‐Scholes options pricing formalism revolutionized options markets when it was published in 1973. It provided the first popular quantitative framework for estimating the fair price of an option according to the contract parameters and the characteristics of the underlying. The Black‐Scholes equation models the price evolution of a European‐style option (an option that can only be exercised at expiration) within the context of the broader financial market. The corresponding Black‐Scholes formula uses this equation to estimate the theoretical price of that option according to its parameters.

It's important to note that the purpose of this Black‐Scholes section is not to elucidate the underlying mathematics of the model, which can be quite complicated. The output of the model is merely a theoretical value for the fair price of an option. In practice, an option's price typically deviates from this value because of market speculation and supply and demand, which this model does not take into account. Rather, it is essential to have at least a superficial grasp of the Black‐Scholes model to understand (1) the foundational assumptions of financial markets and (2) where implied volatility (a gauge for the market's perception of risk) comes from.

The Black‐Scholes model is based on a set of assumptions related to the dynamics of financial assets and the market as a whole. The assumptions are as follows:

● The market is frictionless (i.e., there are no transaction fees).

● Cash can be borrowed and lent in any amount, even fractional, at the risk‐free rate (the theoretical rate of return of an investment with no risk, a macroeconomic variable assumed to be constant).

● There is no arbitrage opportunity (i.e., profits in excess of the risk‐free rate cannot be made without risk).

● Stocks can be bought and sold in any amount, even fractional amounts.

● Stocks do not pay dividends.⁶

● Stock log returns follow Brownian motion with constant drift and volatility (the theoretical mean and standard deviation of annual log returns).

A Brownian motion, or a Wiener process, is a type of stochastic process or a system that experiences random fluctuations as it evolves with time. Traditionally used to describe the positional fluctuations of a particle suspended in fluid at thermal equilibrium,⁷ a standard Wiener process (denoted W(t)) is mathematically defined by the conditions in the grey box. The mathematical definition can be overlooked if preferred, as the intuition behind the mathematics is more crucial for understanding the theoretical foundation of options pricing and follows after.

● (i.e., the process initially begins at location 0).

● is almost surely continuous.

● The increments of , defined as where , are normally distributed with mean 0 and variance (i.e., the steps of the Wiener process are normally distributed with constant mean of 0 and variance of Δt ).

● Disjoint increments of are independent of one another (i.e., the current step of the process is not influenced by the previous steps, nor does it influence the subsequent steps).

Simplified, a Wiener process is a process that follows a random path. Each step in this path is probabilistic and independent of one another. When disjoint steps of equal duration are plotted in a histogram, that distribution is normal with a constant mean and variance. Brownian motion dynamics are driven by this underlying process. These conditions can be best understood visually, which will also demonstrate why this assumption appears in the development of the Black‐Scholes model as an approximation for price dynamics. Figures 1.6 and 1.7 illustrate the characteristics of Brownian motion, and Figure 1.8 illustrates the dynamics of SPY from 2010–2015⁸ for the purposes of comparison.

The price trends of SPY in Figure 1.8(b) appear fairly similar to the Brownian motion cumulative horizontal displacements shown in Figure 1.6(c). The daily returns for SPY are more prone to outlier moves compared to the horizontal displacements of Brownian motion but share some characteristics. The symmetric geometry of the SPY returns histogram bears resemblance to the fairly normal distribution of horizontal displacements, with the tails of the distribution being more prominent as a result of the history of large price moves.

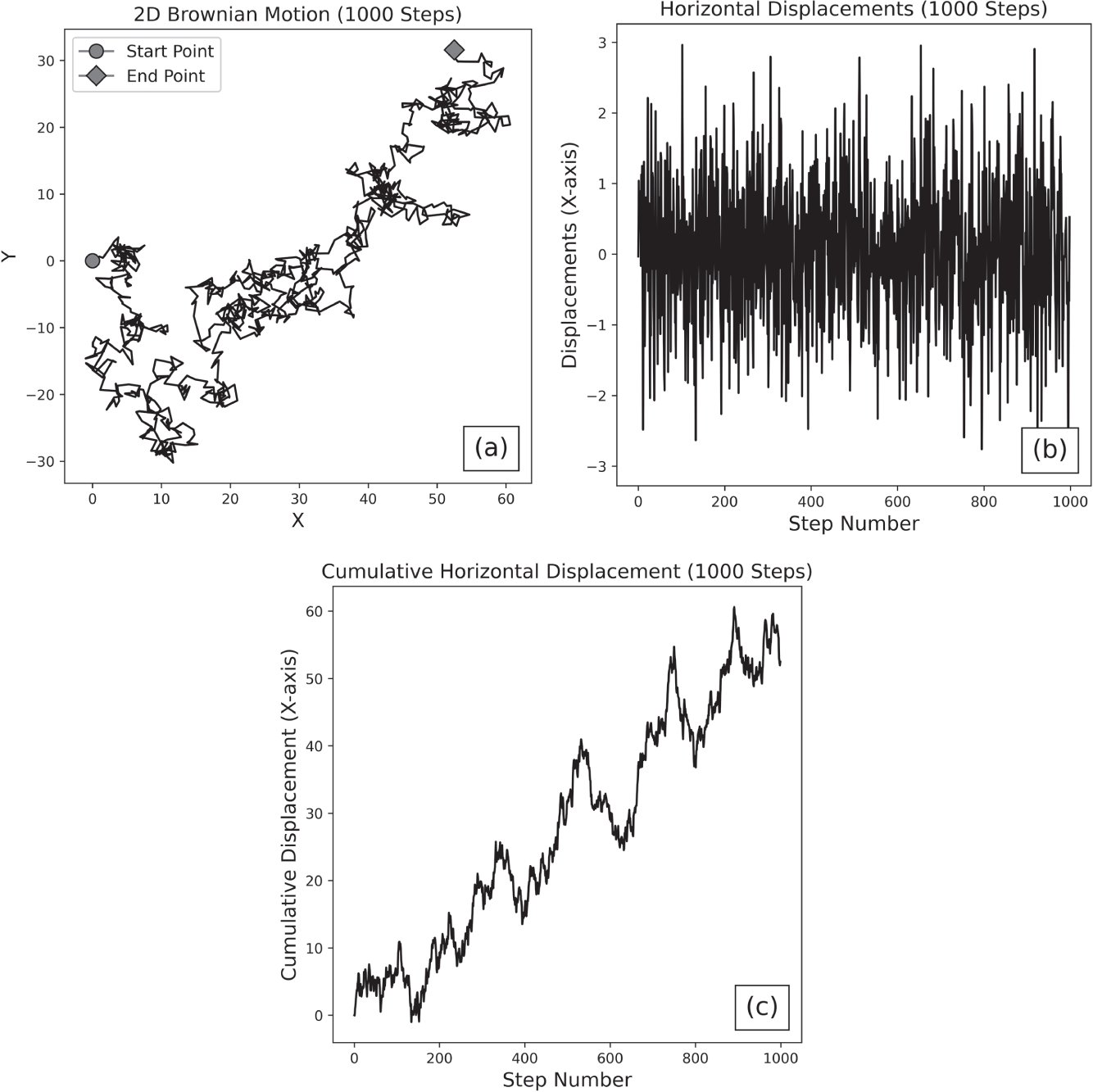
Figure 1.6 (a) The 2D position of a particle in a fluid, moving with Brownian motion. The particle begins at a coordinate of and drifts to a new location over 1,000 steps. (b) The horizontal displacements⁹ of the particle (i.e., the movements of the particle along the X‐axis over 1,000 steps). (c) The cumulative horizontal displacement of the particle over 1,000 steps.

Similarities are clear between price dynamics and Brownian motion, but this remains a highly simplified model of price dynamics. In reality, stock log returns are not normal and are typically skewed to the upside or downside, depending on the specific underlying. Additionally, the drift and volatility of a stock are not directly observable, and it cannot be experimentally confirmed whether or not these variables are constant. Stock volatility approximated with historical return data is rarely constant with time (a phenomenon known as heteroscedasticity). Stock returns are also not typically independent of one another across time (a phenomenon known as autocorrelation), which is a requirement for this model.

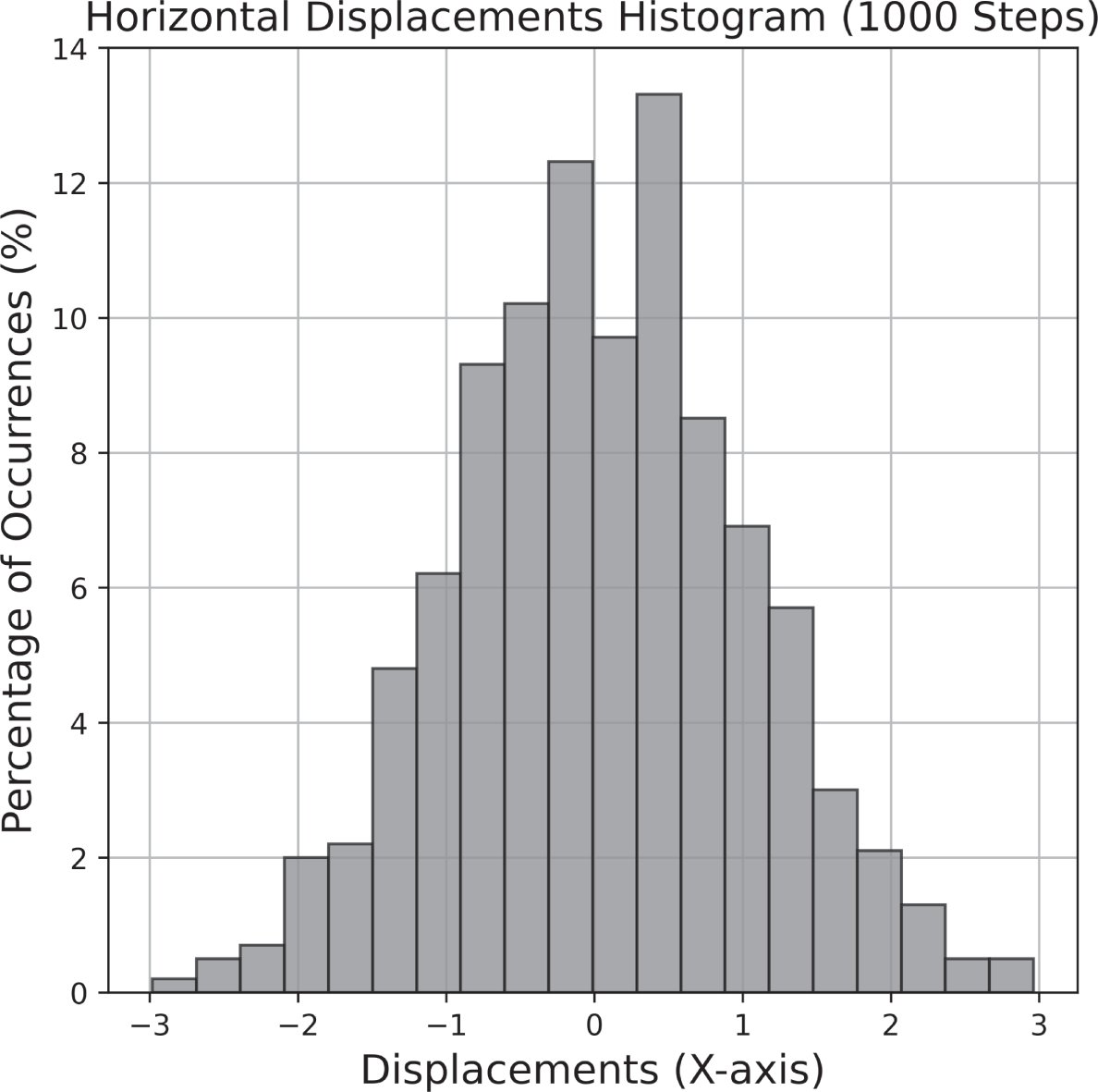
Figure 1.7 The distribution of the horizontal displacements of the particle over 1,000 steps. As characteristic of a Wiener process, the increments are normally distributed, have a mean of zero and variance (which equals 1 in this case). This figure indicates that horizontal step sizes between –1 and 1 are most common, and step sizes with a larger magnitude than 1 are less common.

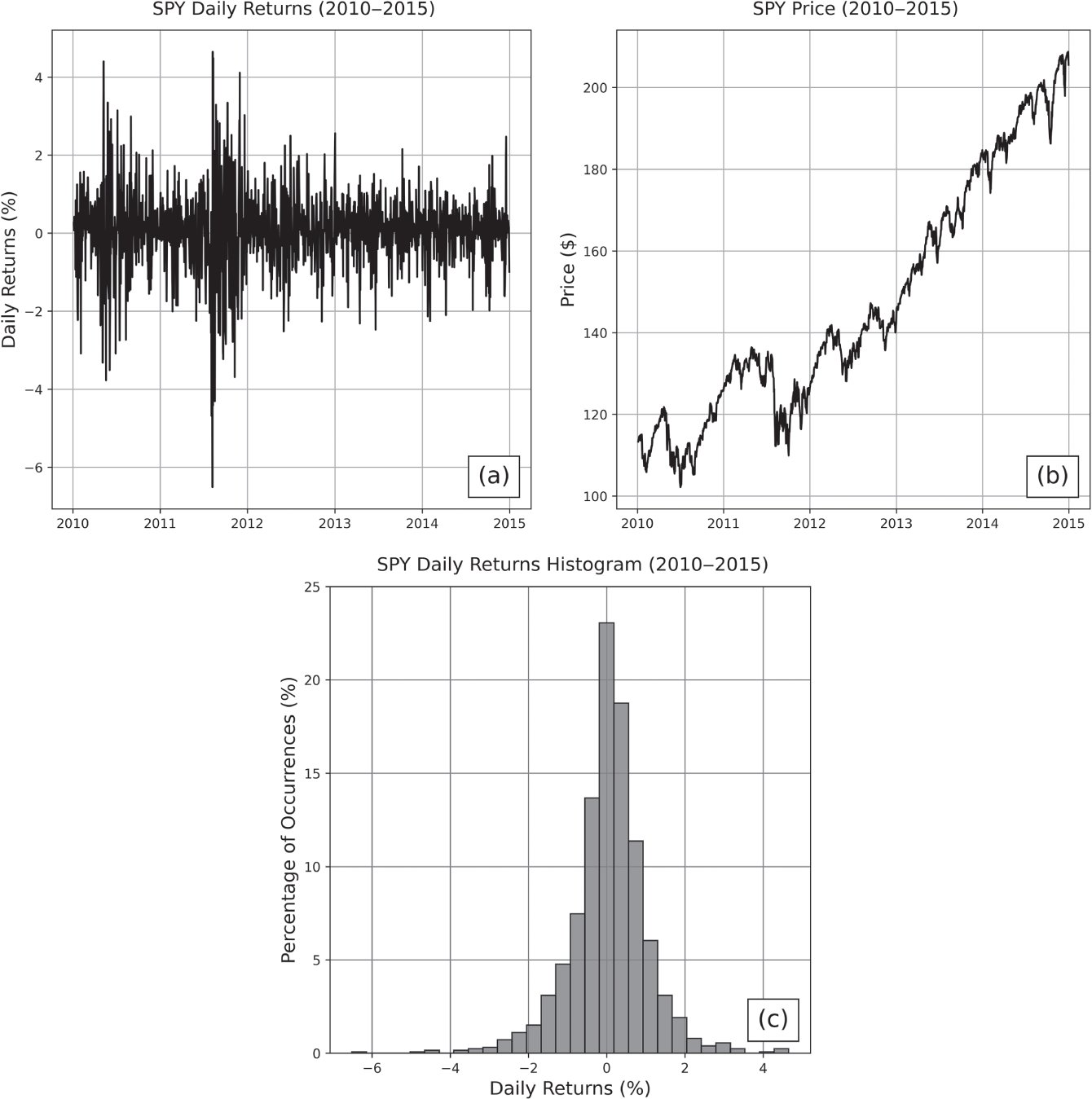
Figure 1.8 The (a) daily returns, (b) price, and (c) daily returns histogram for SPY from 2010–2015.

Although the normality assumption is not entirely accurate, making this simplification allows the development of the rest of this theoretical framework shown in the gray box. The formalism in the gray box is supplemental material for the mathematically inclined. The interpretation of the math, which is more significant, follows after. It should be noted that the Black‐Scholes model technically assumes that stock prices follow geometric Brownian motion, which is more accurate because price movements cannot be negative. Geometric Brownian motion is a slight modification of Brownian motion and requires that the logarithm of the signal follow Brownian motion rather than the signal itself. As it relates to price dynamics, this suggests that the log returns are normally distributed with constant drift (return rate) and volatility.¹⁰

For the price of a stock that follows a geometric Brownian motion, the dynamics of the asset price can be represented with the following stochastic differential equation:¹¹

(1.10)

where is the price of the stock at time t, is the Wiener process at time t , μ is a drift rate, and σ is the volatility of the stock. The drift rate and volatility of the stock are assumed to be constant, and it's important to reiterate that neither of these variables are directly observable. These constants can be approximated using the average return of a stock and the standard deviation of historical returns, but they can never be precisely known.

The equation states that each stock price increment is driven by a predictable amount of drift (with expected return ) and some amount of random noise . In other words, this equation has two components: one that models deterministic price trends and one that models probabilistic price fluctuations . The important takeaway from this observation is that inherent uncertainty is in the price of stock, represented with the contributions from the Wiener process. Because the increments of a Wiener process are independent of one another, it also is common to assume that the weak EMH holds at minimum, in addition to the normality of log returns.

Using this equation as a basis for the derivation, assuming a riskless options portfolio must earn the risk‐free rate, and rearranging terms, the Black‐Scholes equation follows:

(1.11)

where C is the price of a European call (with a dependence on S and t ), S is the price of the stock (with a dependence on t ), r is the risk‐free rate, and σ is the volatility of the stock. The Black‐Scholes formula can be calculated by solving the Black‐Scholes equation according to boundary conditions given by the payoff at expiration of European options. The formula, which provides the value of a European call option for a non‐dividend‐paying stock, is given by the following equation:

(1.12)

where is the value of the standard normal cumulative distribution function at and similarly for , T is the time that the option will expire ( is the duration of the contract), is the price of the stock at time t, K is the strike price of the option, and and are given by the following:

(1.13)

(1.14)

where σ is the volatility of the stock. If the equations seem gross, it's because they are.

Again, the purpose of this section is not to describe the underlying mechanics of the Black‐Scholes model in detail. Rather, Equations (1.10) through (1.14) are included to emphasize three important points.

1. There is inherent uncertainty in the price of stock. Stock price movements are also assumed to be independent of one another and log‐normally distributed.¹²

2. An estimate for the fair price of an option can be calculated according to the price of the stock, the volatility of the stock, the risk‐free rate, the duration of the contract, and the strike price.

3. The volatility of a stock, which plays an important role in estimating the risk of an asset and the valuation of an option, cannot be directly observed. This suggests that the “true risk” of an instrument can never be exactly known. Risk can only be approximated using a metric, such as historical volatility or the standard deviation of the historical returns over some timescale, typically matching the duration of the contract. Other than using a past‐looking metric, such as historical volatility to estimate the risk of an asset, one can also infer the risk of an asset from the price of its options.

As stated previously, the Black‐Scholes model only gives a theoretical estimate for the fair price of an option. Once the contract is traded on the options market, the price of the contract is often driven up or down depending on speculation and perceived risk. The deviation of an option's price from its theoretical value as a result of these external factors is indicative of implied volatility. When initially valuing an option, the historical volatility of the stock has been priced into the model. However, when the price of the option trades higher or lower than its theoretical value, this indicates that the perceived volatility of the underlying deviates from what is estimated by historical returns.

Implied volatility may be the most important metric in options trading. It is effectively a measure of the sentiment of risk for a given underlying according to the supply and demand for options contracts. For an example, suppose a non‐dividend‐paying stock currently trading at $100 per share has a historical 45‐day returns volatility of 20%. Suppose its call option with a 45‐day duration and a strike price of $105 is trading at $2 per share. Plugging these parameters into the Black‐Scholes model, this call option should theoretically be trading at $1 per share. However, demand for this position has increased the contract price significantly. For the model to return a call price of $2 per share, the volatility of this underlying would have to be 28% (assuming all else is constant). Therefore, although the historical volatility of the underlying is only 20%, the perceived risk of that underlying (i.e., the implied volatility) is actually 28%.

To conclude, the primary purpose of this section was not to dive into the math of the Black‐Scholes. These concepts were, instead, introduced to justify the following axioms that are foundational to this book:

● Profits cannot be made without risk.

● Stock log returns have inherent uncertainty and are assumed to follow a normal distribution.

● Stock price movements are independent across time (i.e., future price changes are independent of past price changes, requiring a minimum of the weak EMH).

● Options can theoretically be priced fairly based on the price of the stock, the volatility of the stock, the risk‐free rate, the duration of the contract, and the strike price.

● The volatility of an asset cannot be directly observed, only estimated using metrics like historical volatility or implied volatility.

The Greeks

Other than implied volatility, the Greeks are the most relevant metrics derived from the Black‐Scholes model. The Greeks are a set of risk measures, and each describes the sensitivity of an option's price with respect to changes in some variable. The most essential Greeks for options traders are delta , gamma , and theta .

Delta is one of the most important and widely used Greeks. It is a first‐order¹³ Greek that measures the expected change in the option price given a $1 increase in the price of the underlying (assuming all other variables stay constant). The equation is as follows:

(1.15)

where V is the price of the option (a call or a put) and S is the price of the underlying stock, noting that ∂ is the partial derivative. The value of delta ranges from –1 to 1, and the sign of delta depends on the type of position:

● Long stock: Δ is 1.

● Long call and short put: Δ is between 0 and 1.

● Long put and short call: Δ is between –1 and 0.

For example, the price of a long call option with a delta of 0.50 (denoted 50Δ because that is the total Δ for a one lot, or 100 shares of underlying) will increase by approximately $0.50 per share when the price of the underlying increases by $1. This makes intuitive sense because a long stock, a long call, and a short put are all bullish strategies, meaning they will profit when the underlying price increases. Similarly, because long puts and short calls are bearish, they will take a loss when the underlying price increases.

Delta has a sign and magnitude, so it is a measure of the degree of directional risk of a position. The sign of delta indicates the direction of the risk, and the magnitude of delta indicates the severity of exposure. The larger the magnitude of delta, the larger the profit and loss potential of the contract. This is because positions with larger deltas are closer to/deeper ITM and more sensitive to changes in the underlying price. A contract with a delta of 1.0 (100Δ ) has maximal directional exposure and is maximally ITM. 100Δ options behave like the stock price, as a $1 increase in the underlying creates a $1 increase in the option's price per share. A contract with a delta of 0.0 has no directional exposure and is maximally OTM. A 50Δ contract is defined as having the ATM strike.¹⁴

Because delta is a measure of directional exposure, it plays a large role when hedging directional risks. For instance, if a trader currently has a 50Δ position on and wants the position to be relatively insensitive to directional moves in the underlying, the trader could offset that exposure with the addition of 50 negative deltas (e.g., two 25Δ long puts). The composite position is called delta neutral.

Gamma is a second‐order Greek and a measure of the expected change in the option delta given a $1 change in the underlying price. Gamma is mathematically represented as follows:

(1.16)

As with delta, the sign of gamma depends on the type of position:

● Long call and long put: .

● Short call and short put: .

In other words, if there is a $1 increase in the underlying price, then the delta for all long positions will become more positive, and the delta for all short positions will become more negative. This makes intuitive sense because a $1 increase in the underlying pushes long calls further ITM, increasing the directional exposure of the contract, and it pushes long puts further OTM, decreasing the inverse directional exposure of the contract and bringing the negative delta closer to zero. The magnitude of gamma is highest for ATM positions and lower for ITM and OTM positions, meaning that delta is most sensitive to underlying price movements at –50Δ and 50Δ .

Awareness of gamma is critical when trading options, particularly when aiming for specific directional exposure. The delta of a contract is typically transient, so the gamma of a position gives a better indication of the long‐term directional exposure. Suppose traders wanted to construct a delta neutral position by pairing a short call (negative delta) with a short put (positive delta), and they are considering using 20Δ or 40Δ contracts (all other parameters identical). The 40Δ contracts are much closer to ATM (50Δ ) and have more profit potential than the 20Δ positions, but they also have significantly more gamma risk and are less likely to remain delta neutral in the long term. The optimal choice would then depend on how much risk traders are willing to accept and their profit goals. For traders with high profit goals and a large enough account to handle the large P/L swings and loss potential of the trade, the 40Δ contracts are more suitable.

Theta is a first‐order Greek that measures the expected P/L changes resulting from the decay of the option's extrinsic value (the difference between the current market price for the option and the intrinsic value of the option) per day. It is also commonly referred to as the time decay of the option. Theta is mathematically represented as follows:

(1.17)

where V is the price of the option (a call or a put) and t is time. The sign of theta depends on the type of position and is opposite gamma:

● Long call and long put: .

● Short call and short put: .

In other words, the time decay of the extrinsic value decreases the value of the long position and increases the value of the short position. For instance, a long call with a theta of –5 per one lot is expected to decline in value by $5 per day. This makes intuitive sense because the holders of the contract take gradual losses as their asset depreciates with time, a result of the value of the option converging to its intrinsic value as uncertainty dissipates. Because the extrinsic value of a contract decreases with time, the short side of the position profits with time and experiences positive time decay. The magnitude of theta is highest for ATM options and lower for ITM and OTM positions, all else constant.

There is a trade‐off between the gamma and theta of a position. For instance, a long call with the benefit of a large, positive gamma will also be subjected to a large amount of negative time decay. Consider these examples:

● Position 1: A 45 DTE, 16Δ call with a strike price of $50 is trading on a $45 underlying. The long position has a gamma of 5.4 and a theta of –1.3.

● Position 2: A 45 DTE, 44Δ call with a strike price of $50 is trading on a $49 underlying. The long position has a gamma of 7.9 and a theta of –2.2.

Compared to the first position, the second position has more gamma exposure, meaning that the contract delta (and the contract price) is more sensitive to changes in the underlying price and is more likely to move ITM. However, this position also comes with more theta decay, meaning that the extrinsic value also decreases more rapidly with time.

To conclude this discussion of the Black‐Scholes model and its risk measures, note that the outputs of all options pricing models should be taken with a grain of salt. Pricing models are founded on simplified assumptions of real financial markets. Those assumptions tend to become less representative in highly volatile market conditions when potential profits and losses become much larger. The assumptions and Greeks of the Black‐Scholes model can be used to form reasonable expectations around risk and return in most market conditions, but it's also important to supplement that framework with model‐free statistics.